Reference : Introduction to Algorithms

1. The root is black

   

   • 이진 탐색 트리(Binary Search Tree)의 한 종류

     <aside> 💡 이진 탐색 트리(Binary Search Tree, BST)

     • 이진 탐색(binary search)과 연결리스트(linked list)를 결합한 자료구조의 일종
     • 이진 탐색의 효율적 탐색 능력 $O(log \ n)$을 유지하면서, 빈번한 자료 입력과 삭제를 가능하도록 고안

     이진 탐색 트리의 속성

     1. 각 노드의 왼쪽 서브트리에는 해당 노드의 값보다 작은 값을 지닌 노드들로 이루어져 있음
     2. 각 노드의 오른쪽 서브트리에는 해당 노드의 값보다 큰 값을 지닌 노드들로 이루어져 있음
     3. 중복된 노드가 없어야 함
     4. 왼쪽 서브트리, 오른쪽 서브트리 또한 이진 탐색 트리
     • 이진 탐색 트리를 순회할 때는 중위순회(inorder traversal) 방식을 사용
     • 중위순회(왼쪽 서브트리 - 노드 - 오른쪽 서브트리)를 통해 BST 내에 있는 모든 값들을 정렬된 순서대로 읽을 수 있음

     이진 탐색 트리의 연산

     • 검색(retrieve)
     • 삽입(insert)
     • 삭제(delete) 위 3가지의 연산 모두 $O(h)$로, 트리의 높이에 의해 수행시간이 결정되는 구조 (imbalanced) → 이 때문에 트리의 입력/삭제 단계에 트리 전체의 균형을 맞추는 AVL Tree 제안

     </aside>

   • 스스로 균형(balancing) 잡는 트리

   • BST의 worst case의 단점 개선

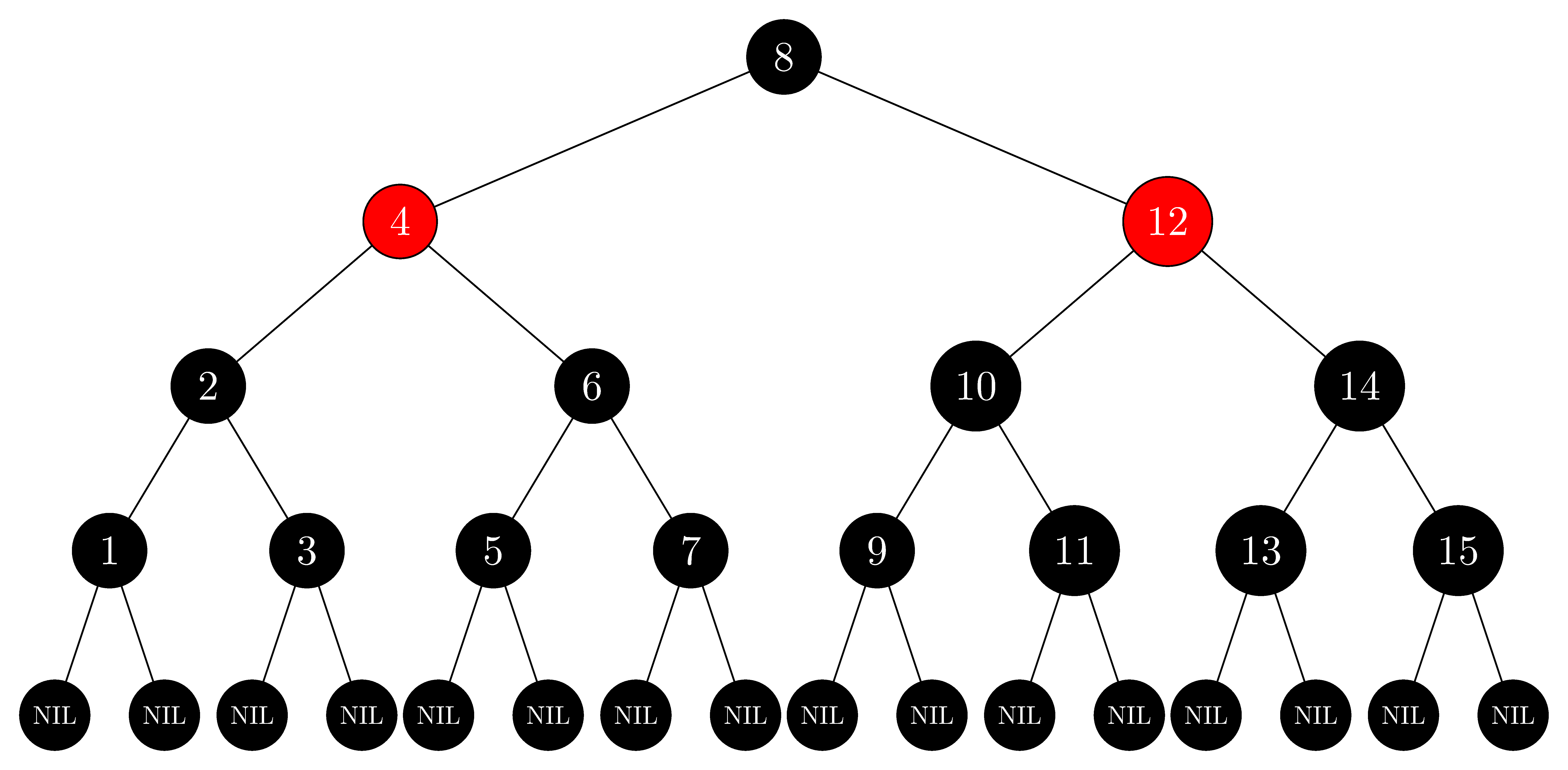
     • 모든 노드는 Red or Black

   Red-Black properties

   1. Every node is either Red or Black

2. Every leaf (NIL) is black.

3. If a node is red, then both its children are black.

   (= red가 연속적으로 존재할 수 없다)

4. For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.

   → 각 노드에서 leaf node 까지 가는 경로의 black node의 수는 항상 같아야 한다. (자기 자신 제외)

<aside> 💡 NIL Node

• 존재하지 않음을 의미하는 노드
• 자녀가 없을 때 자녀를 nil노드로 표기
• 값이 있는 노드와 동등하게 취급
• RB 트리에서 leaf 노드는 nil 노드

</aside>

Balancing : RB 트리는 어떻게 균형을 잡는가?

삽입/삭제 시 주로 property #4, #5를 위반하며, 위반 사항들을 해결하고자 트리의 구조를 바꾸다 보면 트리가 균형을 이루게 됨

#4 : 노드가 red라면 자식은 black

#5 : 각 노드에서 leaf node에 도달하는 경로의 black node 수는 항상 같아야 함

RB Tree - Rotations

Time Complexity of Search-tree operation (TREE-INSERT, TREE-DELETE) : $O(log\ n)$

$\because$ Modified tree may violate the red-black properties

to restore RB properties, colors and pointers within node need to change

→ The pointer structure changes through rotation

Left-Rotate(T, x)
		y = x.right
		x.right = y.left
	
		if y.left != T.nil
				y.left.p = x
		y.p = x.p

		if x.p == T.nil
				T.root = y
		
		else if x == x.p.left
				x.p.left = y
		
		else 
				x.p.right = y
		
		y.left = x
		x.p = y

Right-Rotate(T, y)
		x = y.left
		y.left = x.right
		
		if x.right != T.nil
				x.right.p = y
		x.p = y.p

		if y.p == T.nil
				t.root = x
		
		else if y == y.p.left
				y.p.left = x
		
		else
				y.p.right = x
		
		x.right = y
		y.p = x